homework 7, version 1

Submission by: Jazzy Doe (jazz@mit.edu)

Homework 7: Raytracing in 2D

18.S191, fall 2020

This notebook contains built-in, live answer checks! In some exercises you will see a coloured box, which runs a test case on your code, and provides feedback based on the result. Simply edit the code, run it, and the check runs again.

For MIT students: there will also be some additional (secret) test cases that will be run as part of the grading process, and we will look at your notebook and write comments.

Feel free to ask questions!

Let's create a package environment:

Exercise 1: Walls

As discussed the lecture, event-driven simulations are the traditional method used for raytracing. Here, we look for any objects in our path and analytically determine how far away they are. From there, we take one big timestep all the way to the surface boundary, calculate refraction or reflection to see what direction we are moving in, and then seek out any other object we could potentially run into.

So let's start simple with determining when a ray of light could intersect with a wall.

Exercise 1.1 - what is a wall?

To start, let's create the concept of a wall. For our purposes, walls will be infinitely long, so we only need to create an object that has a position and a normal vector at that position:

In our simulations, we will enclose our scene in a box of four walls, to make sure that no rays can escape the scene. We have written this box (i.e. vector of walls) below, but we are still missing the roof.

👉 Modify the definition of box_scene to be a vector of 4 walls, instead of 3. The fourth wall should be positioned at [0,10], and point downwards.

In the next exercise, we will find the intersection of a ray of light and a wall. To represent light, we create a struct called Photon, holding the position and travel direction of a single particle of light. We also include the index of refraction of the medium it is currently traveling in, we will use this later.

Exercise 1.2 - how far is the wall?

We will write a function that finds the location where a photon hits the wall. Instead of moving the photon forward in small timesteps until we reach the wall, we will compute the intersection directly, making use of the fact that the wall is a geometrically simple object.

Our function will return one of two possible types: a Miss or a Intersection. We define these types below, and both definitions need some elaboration.

Miss

is a struct with no fields. It does not contain any information, except the fact that it is a Miss. You create a new Miss object like so:

Intersection

is a parametric type. The first field (object) is of type T, and T is a subtype of Object. Have a look at the definition above, and take note of how we write such statements in Julia syntax.

We also could have used Object directly as the type for the field object, but what's special about parametric types is that T becomes "part of the type". Let's have a look at an example:

You see that Wall is included in the type. This will be very useful later, when we want to do something different depending on the intersected object (wall, sphere, etc.) using multiple dispatch. We can write one method for ::Intersection{Sphere}, and one for ::Intersection{Wall}.

Wall geometry

So, how do we find the location where it hits the wall? Well, because our walls are infinitely long, we are essentially trying to find the point at which 2 lines intersect.

To do this, we can combine a few dot products: one to find how far away we are, and another to scale that distance. Mathematically, it would look like:

$$D=-\frac{(p_{\text{ray}}-p_{\text{wall}})\cdot \hat{n}}{\hat{\ell }\cdot \hat{n}},$$

where $p$ is the position, $\hat{\ell }$ is the direction of the light, and $\hat{n}$ is the normal vector for the wall. subscripts $i$, $r$, and $w$ represent the intersection point, ray, and wall respectively. The result is $D$, the amount that the photon needs to travel until it hits the wall.

👉 Write a function intersection_distance that implements this formula, and returns $D$. You can use dot(a,b) to compute the vector dot product $a\cdot b$.

Exercise 1.3 - hitting the wall

👉 Write a function intersection that takes a photon and a wall, and returns either a Miss or an Intersection, based on the result of intersection_distance(photon, wall) $=D$.

If $D$ is positive, then the photon will hit the wall, and we should return an Intersection. We already have the intersected object, and we have $D$, our intersection distance. To find the intersection point, we use the photon's position and velocity.

$$p_{\text{intersection}}=p_{\text{ray}}+D\hat{\ell }$$

If $D$ is negative (or zero), then the wall is behind the photon - we should return a Miss.

Floating points

We are using floating points (Float64) to store positions, distances, etc., which means that we need to account for small errors. Like in the lecture, we will not check for D > 0, but D > ϵ with ϵ = 1e-3.

Exercise 1.4 - which wall?

We are now able to find the Intersection of a single photon with a single wall (or detect a Miss). Great! To make our simulation more interesting, we will combine multiple walls into a single scene.

When we shoot a photon at the scene, we compute the intersections between the photon and every object in the scene. Click on the vector below to see all elements:

There are two misses and three intersections. Just what we hoped!

So which of these five results should we use to determine what the photon does next? It should be the closest intersection.

Because we used two different types for hits and misses, we can express this in a charming way. We define what it means for one to be better than the other:

And we can now use all of Julia's built in functions to work with a vector of hit/miss results. For example, we can sort it:

And we can take the minimum:

Note that we did not define the sort and minimum methods ourselves! We only added methods for Base.isless.

By taking the minimum, we have found our closest hit! Let's turn this into a function.

👉 Write a function closest_hit that takes a photon and a vector of objects. Calculate the vector of Intersections/Misses, and return the minimum.

Exercise 2: Mirrors

Now we're going to make a bold claim: All walls in this simulation are mirrors. This is just for simplicity so we don't need to worry about rays stopping at the boundaries.

We are already able to find the intersection of a light ray with a mirror, but we still need to tell our friendly computer what a reflection is.

Exercise 2.1 - reflect

For this one, we need to implement a reflection function. This one is way easier than refraction. All we need to do is find how much of the light is moving in the direction of the surface's normal and subtract that twice.

$${\ell }_2={\ell }_1-2({\ell }_1\cdot \hat{n})\hat{n}$$

Where ${\ell }_1$ and ${\ell }_2$ are the photon directions before and after the reflection off a surface with normal $\hat{n}$. Let's write that in code:

👉 Verify that the function reflect works by writing a simple test case:

Exercise 2.2 - step

Our event-driven simulation is a stepping method, but instead of taking small steps in time, we take large steps from one collision event to the next.

👉 Write a function interact that takes a photon and a hit::Intersection{Wall} and returns a new Photon at the next step. The new photon is located at the hit point, its direction is reflected off the wall's normal and the photon.ior is reused.

For convenience, we define a function step_ray that combines these two actions: it finds the closest hit and computes the interaction.

Great! Next, we will repeat this action to trace the path of a photon.

Exercise 2.3 - accumulate

👉 Write a function trace that takes an initial Photon, a vector of Objects and N, the number of steps to make. Return a vector of Photons. Try to use accumulate.

Recap

In Exercise 3 and 4, we will add a Sphere type, and our scene will consist of Walls (mirrors) and Spheres (lenses). But before we move on, let's review what we have done so far.

Our main character is a Photon, which bounces around a scene made up of Walls.

1. Using intersection(photon, wall::Wall) we can find either an Intersection (containing the wall, the distance and the point) or a Miss.

2. Our scene is just a Vector or objects, and we compute the intersection between the photon and every object.

3. By adding Base.isless methods we have told Julia how to compare hit/miss results, and we get the closest one using minimum(all_intersections).

4. We wrote a function interact(photon, hit::Intersection{Wall}) that returns a new photon after interacting with a wall collision.

We repeat these four steps to trace a ray through the scene.

In the next two exercises we will reuse some of the functionality that we have already written, using multiple dispatch! For example, we add a method intersection(photon, sphere::Sphere), and steps 2 and 3 magically also work with spheres!

Exercise 3: Spheres

Now that we know how to bounce light around mirrors, we want to simulate a spherical lens to make things more interesting. Let's define a Sphere.

Exercise 3.1

Just like with the Wall, our first step is to be able to find the intersection point of a ray of light and a sphere.

This one is a bit more challenging than the intersction with the wall, in particular because there are 3 potential outcomes of a line interacting with a sphere:

• No intersection

• 1 intersection

• 2 intersections

As shown below:

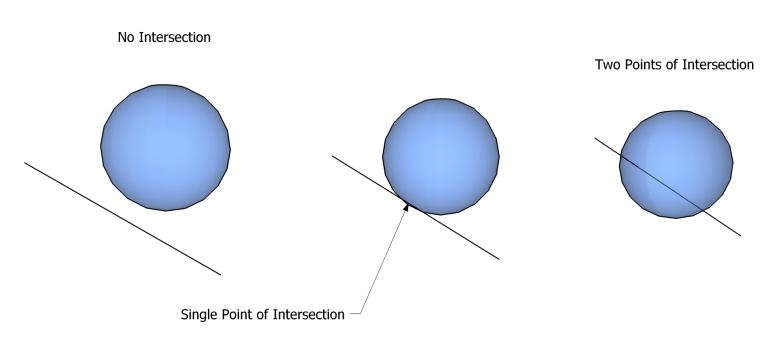
So we need a way of finding all of these.

To start, let's look at the intersection of a point and a sphere. So long as the relative distance between the photon and the sphere's center satisfies the sphere equation, we can be considered inside of the sphere. More specifically, we are inside the sphere if:

$$(x_s-x_p{)}^2+(y_s-y_p)<r^2.$$

where the $s$ and $p$ subscripts represent the sphere and photon, respectively. We know we are on the sphere if

$$(x_s-x_p{)}^2+(y_s-y_p)=r^2.$$

Let's rewrite this in vector notation as:

$$(\mathbf{R}-\mathbf{S})\cdot (\mathbf{R}-\mathbf{S})=r^2,$$

where $\mathbf{R}$ and $\mathbf{S}$ are the $x$, $y$, and $z$ location of the photon and sphere, respectively.

Returning to the timestepping example from above, we know that our ray is moving forward with time such that $\mathbf{R}={\mathbf{R}}_0+vdt={\mathbf{R}}_0+\ell t$. We now need to ask ourselves if there is any time when our ray interacts with the sphere. Plugging this in to the dot product from above, we get

$$({\mathbf{R}}_0+\ell t-\mathbf{S})\cdot ({\mathbf{R}}_0+\ell t-\mathbf{S})=r^2$$

To solve this for $t$, we first need to reorder everything into the form of a polynomial, such that:

$$t^2(\ell \cdot \ell )+2t\ell \cdot ({\mathbf{R}}_{\mathbf{0}}-\mathbf{S})+({\mathbf{R}}_0-\mathbf{S})\cdot ({\mathbf{R}}_0-\mathbf{S})-r^2=0.$$

This can be solved with the good ol' fashioned quadratic equation:

$$\frac{-b\pm \sqrt{b^2-4ac}}{2a},$$

where $a=\ell \cdot \ell$, $b=2\ell \cdot ({\mathbf{R}}_0-\mathbf{S})$, and $c=({\mathbf{R}}_0-\mathbf{S})\cdot ({\mathbf{R}}_0-\mathbf{S})-r^2$

If the quadratic equation returns no roots, there is no intersection. If it returns 1 root, the ray just barely hits the edge of the sphere. If it returns 2 roots, it goes right through!

The easiest way to check this is by looking at the discriminant $d=b^2-4ac$.

$$\text{Number of roots}=\{\begin{array}{rl}& 0,\text{if }d<0\\ & 1,\text{if }d=0\\ & 2,\text{if }d>0\end{array}$$

In the case that there are 2 roots, the second root corresponds to when the ray would interact with the far edge of the sphere if there were no refraction or reflection!; therefore, we only care about returning the closest point.

With all this said, we are ready to write some code.

👉 Write a new method intersection that takes a Photon and a Sphere, and returns either a Miss or an Intersection, using the method described above. Go back to Exercise 1.3 where we defined the first method, and see how we adapt it to a sphere.

👉 Change the definition of test_sphere to test different situations:

• Hit the circle

• Miss the circle

• Start inside the cricle (you should hit the exit boundary)

Exercise 4: Lenses

For this, we will start with refraction from the surface of water and then move on to a spherical lens.

So, how does refraction work? Well, every time light enters a new medium that is more dense than air, it will bend towards the normal to the surface, like so:

This can be described by Snell's law:

$$\frac{n_1}{n_2}=\frac{v_2}{v_1}=\frac{\sin ({\theta }_2)}{\sin ({\theta }_1)}$$

Here, $n$ is the index of refraction, $v$ is the speed (not velocity (sorry for the notation!)), and $\theta$ is the angle with respect to the surface normal. Any variables with an subscript of 1 are in the outer medium (air), and any variables with a subscript 2 are in the inner medium (water).

This means that we can find the angle of the new ray of light as

$$\sin ({\theta }_2)=\frac{n_1}{n_2}\sin ({\theta }_1)$$

The problem is that $\sin$ is slow, so we typically want to rewrite this in terms of vector operations. This means that we want to rewrite everything to be in terms of dot products, but because $A\cdot B=|A||B|cos(\theta )$, we really want to rewrite everything in terms of cosines first. So, using the fact that $\sin (\theta {)}^2+\cos (\theta {)}^2=1$, we can rewrite the above equation to be:

$$\sin ({\theta }_2)=\frac{n_1}{n_2}\sqrt{1-\cos ({\theta }_1{)}^2}$$

We also know that

$$\cos ({\theta }_2)=\sqrt{1-\sin ({\theta }_2{)}^2}=\sqrt{1-{\left(\frac{n_1}{n_2}\right)}^2(1-\cos ({\theta }_1{)}^2)}.$$

Finally, we know that the new light direction should be the same as the old one, but shifted towards (or away) from the normal according to the new refractive index. In particular:

$$n_2{\ell }_2=n_1{\ell }_1+(n_1\cos ({\theta }_1)-n_2\cos ({\theta }_2))\hat{n},$$

where $\hat{n}$ is the normal from the water's surface. Rewriting this, we find:

$${\ell }_2=\left(\frac{n_1}{n_2}\right){\ell }_1+(\left(\frac{n_1}{n_2}\right)\cos ({\theta }_1)-\cos ({\theta }_2))\hat{n}.$$

Now, we already know $\cos ({\theta }_2)$ in terms of $\cos ({\theta }_1)$, so we can just plug that in... But first, let's do some simplifications, such that

$$r=\frac{n_1}{n_2}$$

and

$$c=-\hat{n}\cdot {\ell }_1.$$

Now, we can rewrite everything such that

$${\ell }_2=r{\ell }_1+(rc-\sqrt{1-r^2(1-c^2)})\hat{n}.$$

The last step is to write this in code with a function that takes the light direction, the normal, and old and new indices of refraction:

We need a helper functions to find the normal of the sphere's surface at any position. Remember that the normal will always be pointing perpendicularly from the surface of the sphere. This means that no matter what point you are at, the normal will just be a normalized vector of your current location minus the sphere's position:

👉 Write a new method for interact that takes a photon and a hit of type Intersection{Sphere}, that implements refraction. It returns a new Photon positioned at the hit point, with the refracted velocity and the new index of refraction.

To test your code, modify the definition of test_lens_photon and test_lens below.

By defining a method for interact that takes a sphere intersection, we are now able to use the machinery developed in Exercise 2 to simulate a scene with both lenses and mirrors. Let's try it out!

Spherical aberration

Now we can put it all together into an image of spherical aberration!

👉 Recreate the spherical aberration figure from the lecture (around the end of the video), and make the index of refraction interactive using a Slider. Or make something else!

Exercise XX: Lecture transcript

(MIT students only) Please see the link for hw 7 transcript document on Canvas. We want each of you to correct about 500 lines, but don’t spend more than 20 minutes on it. See the the beginning of the document for more instructions.

👉 Please mention the name of the video(s) and the line ranges you edited:

Function library

Just some helper functions used in the notebook.